SVM model
svm.Rmd
library(rvfl)
glmGamma <- function(formula, ...) {
e1071::svm(formula = formula, ...)
}Example 1: MPG Prediction (mtcars dataset)
Fit models
# Fit regular linear model
start <- proc.time()[3]
lm_model <- lm(mpg ~ ., data = train_data)
print(proc.time()[3] - start)## elapsed
## 0.011##
## Call:
## lm(formula = mpg ~ ., data = train_data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.5211 -0.9792 -0.0324 1.1808 4.9814
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -5.054416 25.456900 -0.199 0.8455
## cyl 0.695392 1.396506 0.498 0.6262
## disp 0.005254 0.017342 0.303 0.7664
## hp -0.007610 0.027723 -0.274 0.7877
## drat 4.128157 2.724353 1.515 0.1520
## wt -1.621396 2.139071 -0.758 0.4610
## qsec 0.064356 0.932144 0.069 0.9459
## vs 0.138716 3.421183 0.041 0.9682
## am -0.498476 2.956568 -0.169 0.8685
## gear 4.402648 2.287816 1.924 0.0749 .
## carb -1.999389 1.299580 -1.538 0.1462
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.464 on 14 degrees of freedom
## Multiple R-squared: 0.8938, Adjusted R-squared: 0.818
## F-statistic: 11.79 on 10 and 14 DF, p-value: 3.4e-05## 2.5 % 97.5 %
## (Intercept) -59.65403559 49.54520296
## cyl -2.29981561 3.69060001
## disp -0.03194096 0.04244882
## hp -0.06707095 0.05185084
## drat -1.71500030 9.97131342
## wt -6.20924769 2.96645550
## qsec -1.93489537 2.06360651
## vs -7.19899241 7.47642359
## am -6.83968216 5.84273112
## gear -0.50422869 9.30952400
## carb -4.78671119 0.78793282
# Fit calibrated model
start <- proc.time()[3]
svm_model <- rvfl::calibmodel(lambda=10**seq(-10, 10, length.out=100), x = as.matrix(train_data[,-1]), y = train_data$mpg, engine = glmGamma)
print(proc.time()[3] - start)## elapsed
## 0.18##
## Call:
## svm(formula = formula, data = ..1)
##
##
## Parameters:
## SVM-Type: eps-regression
## SVM-Kernel: radial
## cost: 1
## gamma: 0.1
## epsilon: 0.1
##
##
## Number of Support Vectors: 22
#print(confint(svm_model$model))
#print(simulate(svm_model, newdata = test_data))Compare predictions
results <- data.frame(
Actual = mtcars[-train_idx, ]$mpg,
LM_Pred = lm_pred[,"fit"],
LM_Lower = lm_pred[,"lwr"],
LM_Upper = lm_pred[,"upr"],
svm_Pred = svm_pred[,"fit"],
svm_Lower = svm_pred[,"lwr"],
svm_Upper = svm_pred[,"upr"]
)
# Print results
print("Prediction Intervals Comparison:")## [1] "Prediction Intervals Comparison:"## Actual LM_Pred LM_Lower LM_Upper svm_Pred svm_Lower svm_Upper
## Valiant 18.1 17.93324 10.149847 25.71663 21.33478 15.06733 26.60367
## Merc 280C 17.8 20.63530 13.636618 27.63398 20.86656 15.31682 26.85315
## Toyota Corolla 33.9 28.58373 22.379666 34.78779 28.16744 22.61770 34.15404
## Camaro Z28 13.3 15.85710 8.140858 23.57335 18.65393 13.10419 24.64052
## Porsche 914-2 26.0 31.07535 18.988702 43.16201 23.89842 18.42376 29.96010
## Ford Pantera L 15.8 27.07516 14.930150 39.22016 21.36127 15.81153 27.34786
# Calculate coverage and Winkler scores
lm_coverage <- mean(mtcars[-train_idx, ]$mpg >= results$LM_Lower &
mtcars[-train_idx, ]$mpg <= results$LM_Upper)
svm_coverage <- mean(mtcars[-train_idx, ]$mpg >= results$svm_Lower &
mtcars[-train_idx, ]$mpg <= results$svm_Upper)
lm_winkler <- misc::winkler_score(mtcars[-train_idx, ]$mpg, results$LM_Lower, results$LM_Upper)
svm_winkler <- misc::winkler_score(mtcars[-train_idx, ]$mpg, results$svm_Lower, results$svm_Upper)
print(sprintf("\nPrediction interval metrics:"))## [1] "\nPrediction interval metrics:"
print(sprintf("Linear Model: %.1f%% coverage, %.3f Winkler score",
100 * lm_coverage, mean(lm_winkler)))## [1] "Linear Model: 100.0% coverage, 18.226 Winkler score"
print(sprintf("Calibrated Model: %.1f%% coverage, %.3f Winkler score",
100 * svm_coverage, mean(svm_winkler)))## [1] "Calibrated Model: 71.4% coverage, 17.780 Winkler score"
sims <- simulate(svm_model, newdata = as.matrix(test_data), nsim = 500, method="bootstrap")
# Plot simulations
matplot(sims, type = "l",
col = rgb(0, 0, 1, 0.1), lty = 1,
xlab = "obs. #", ylab = "Simulated MPG",
main = "Ridge Model Simulations")
lines(mtcars[-train_idx, ]$mpg, col = "red") 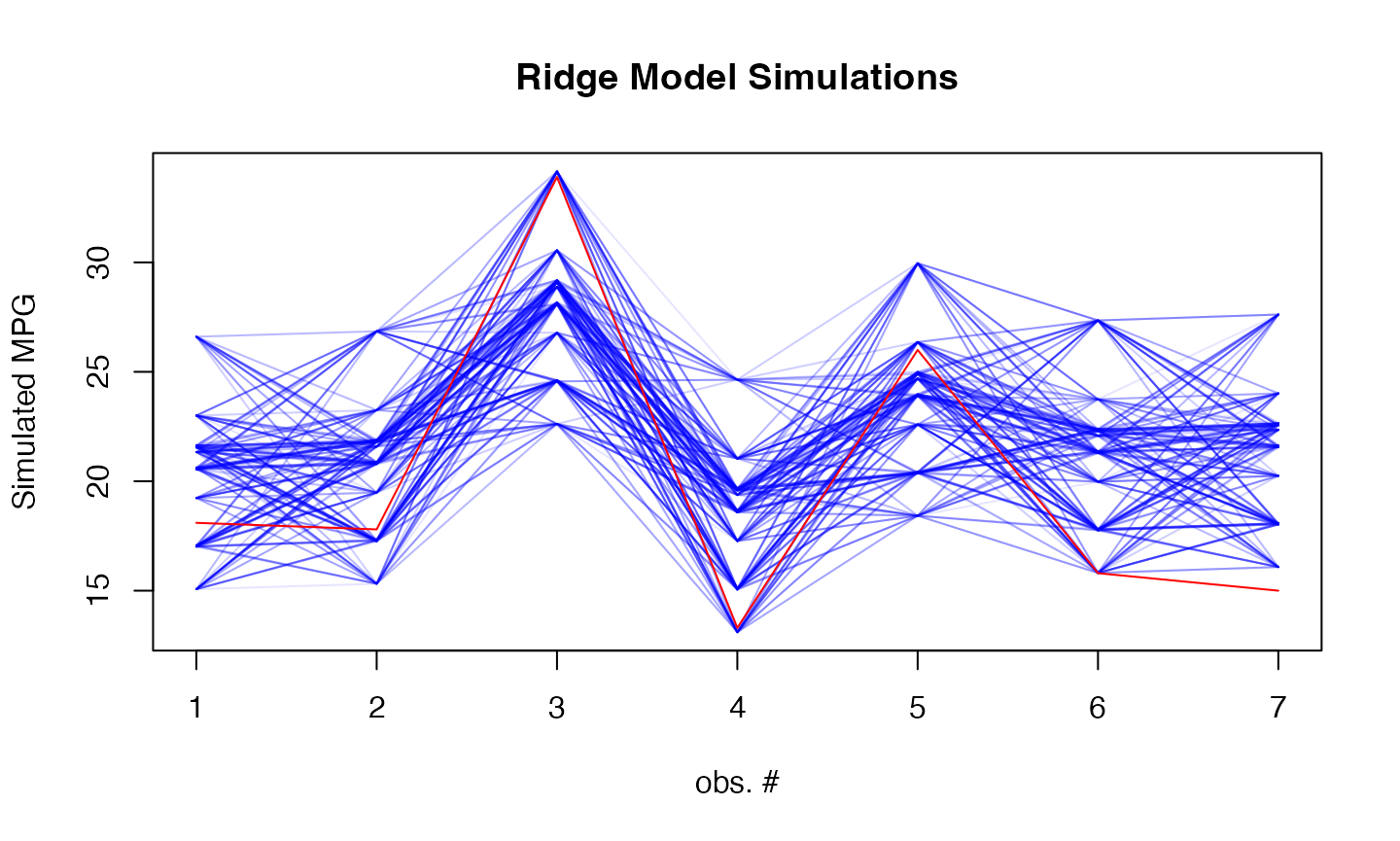
Example 2: Boston Housing Price Prediction
Fit models
# Fit regular linear model
start <- proc.time()[3]
lm_model <- lm(medv ~ ., data = train_data)
print(proc.time()[3] - start)## elapsed
## 0.009##
## Call:
## lm(formula = medv ~ ., data = train_data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -15.220 -2.757 -0.494 1.863 26.961
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 35.832339 5.763210 6.217 1.30e-09 ***
## crim -0.095389 0.034717 -2.748 0.006282 **
## zn 0.042689 0.016086 2.654 0.008283 **
## indus -0.033013 0.073521 -0.449 0.653657
## chas 2.506064 0.939731 2.667 0.007977 **
## nox -17.521010 4.237379 -4.135 4.35e-05 ***
## rm 3.966727 0.477640 8.305 1.66e-15 ***
## age 0.006479 0.014922 0.434 0.664410
## dis -1.463187 0.232348 -6.297 8.17e-10 ***
## rad 0.253984 0.075379 3.369 0.000828 ***
## tax -0.009853 0.004350 -2.265 0.024068 *
## ptratio -1.002914 0.147016 -6.822 3.44e-11 ***
## black 0.008723 0.002984 2.923 0.003664 **
## lstat -0.501984 0.057704 -8.699 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 4.835 on 390 degrees of freedom
## Multiple R-squared: 0.7403, Adjusted R-squared: 0.7316
## F-statistic: 85.51 on 13 and 390 DF, p-value: < 2.2e-16## 2.5 % 97.5 %
## (Intercept) 24.50149090 47.16318623
## crim -0.16364441 -0.02713269
## zn 0.01106383 0.07431451
## indus -0.17755967 0.11153316
## chas 0.65849254 4.35363615
## nox -25.85197459 -9.19004505
## rm 3.02765548 4.90579898
## age -0.02285933 0.03581667
## dis -1.91999833 -1.00637601
## rad 0.10578379 0.40218383
## tax -0.01840515 -0.00129986
## ptratio -1.29195676 -0.71387117
## black 0.00285660 0.01458927
## lstat -0.61543411 -0.38853422
# Fit calibrated model
start <- proc.time()[3]
svm_model <- rvfl::calibmodel(lambda=10**seq(-10, 10, length.out=100), x = as.matrix(train_data[,-14]), y = train_data$medv, engine = glmGamma)
print(proc.time()[3] - start)## elapsed
## 0.092##
## Call:
## svm(formula = formula, data = ..1)
##
##
## Parameters:
## SVM-Type: eps-regression
## SVM-Kernel: radial
## cost: 1
## gamma: 0.07692308
## epsilon: 0.1
##
##
## Number of Support Vectors: 147Make predictions and compare
results <- data.frame(
Actual = Boston[-train_idx, ]$medv,
LM_Pred = lm_pred[,"fit"],
LM_Lower = lm_pred[,"lwr"],
LM_Upper = lm_pred[,"upr"],
svm_Pred = svm_pred[,"fit"],
svm_Lower = svm_pred[,"lwr"],
svm_Upper = svm_pred[,"upr"]
)
# Print results
print("Prediction Intervals Comparison:")## [1] "Prediction Intervals Comparison:"## Actual LM_Pred LM_Lower LM_Upper svm_Pred svm_Lower svm_Upper
## 1 24.0 30.57209 20.958399 40.18579 28.85933 24.333712 37.61434
## 3 34.7 30.68339 21.107377 40.25940 32.92264 23.340798 42.66320
## 4 33.4 28.70511 19.107688 38.30253 31.68660 26.522509 41.24607
## 18 17.5 17.06191 7.487523 26.63630 16.95144 9.299141 25.05877
## 21 13.6 12.85420 3.239688 22.46872 14.40651 9.001747 24.53908
## 24 14.5 14.14956 4.535627 23.76348 15.06066 9.452245 26.41643
# Calculate coverage and Winkler scores
lm_coverage <- mean(Boston[-train_idx, ]$medv >= results$LM_Lower &
Boston[-train_idx, ]$medv <= results$LM_Upper)
svm_coverage <- mean(Boston[-train_idx, ]$medv >= results$svm_Lower &
Boston[-train_idx, ]$medv <= results$svm_Upper)
lm_winkler <- misc::winkler_score(Boston[-train_idx, ]$medv, results$LM_Lower, results$LM_Upper)
svm_winkler <- misc::winkler_score(Boston[-train_idx, ]$medv, results$svm_Lower, results$svm_Upper)
print(sprintf("\nPrediction interval metrics:"))## [1] "\nPrediction interval metrics:"
print(sprintf("Linear Model: %.1f%% coverage, %.3f Winkler score",
100 * lm_coverage, mean(lm_winkler)))## [1] "Linear Model: 95.1% coverage, 26.711 Winkler score"
print(sprintf("Calibrated Model: %.1f%% coverage, %.3f Winkler score",
100 * svm_coverage, mean(svm_winkler)))## [1] "Calibrated Model: 96.1% coverage, 27.987 Winkler score"
sims <- simulate(svm_model, newdata = as.matrix(test_data), nsim = 500, method="bootstrap")
# Plot simulations
matplot(sims, type = "l",
col = rgb(0, 0, 1, 0.1), lty = 1,
xlab = "obs. #", ylab = "Simulated MPG",
main = "Ridge Model Simulations")
lines(Boston[-train_idx, ]$medv, col = "red") 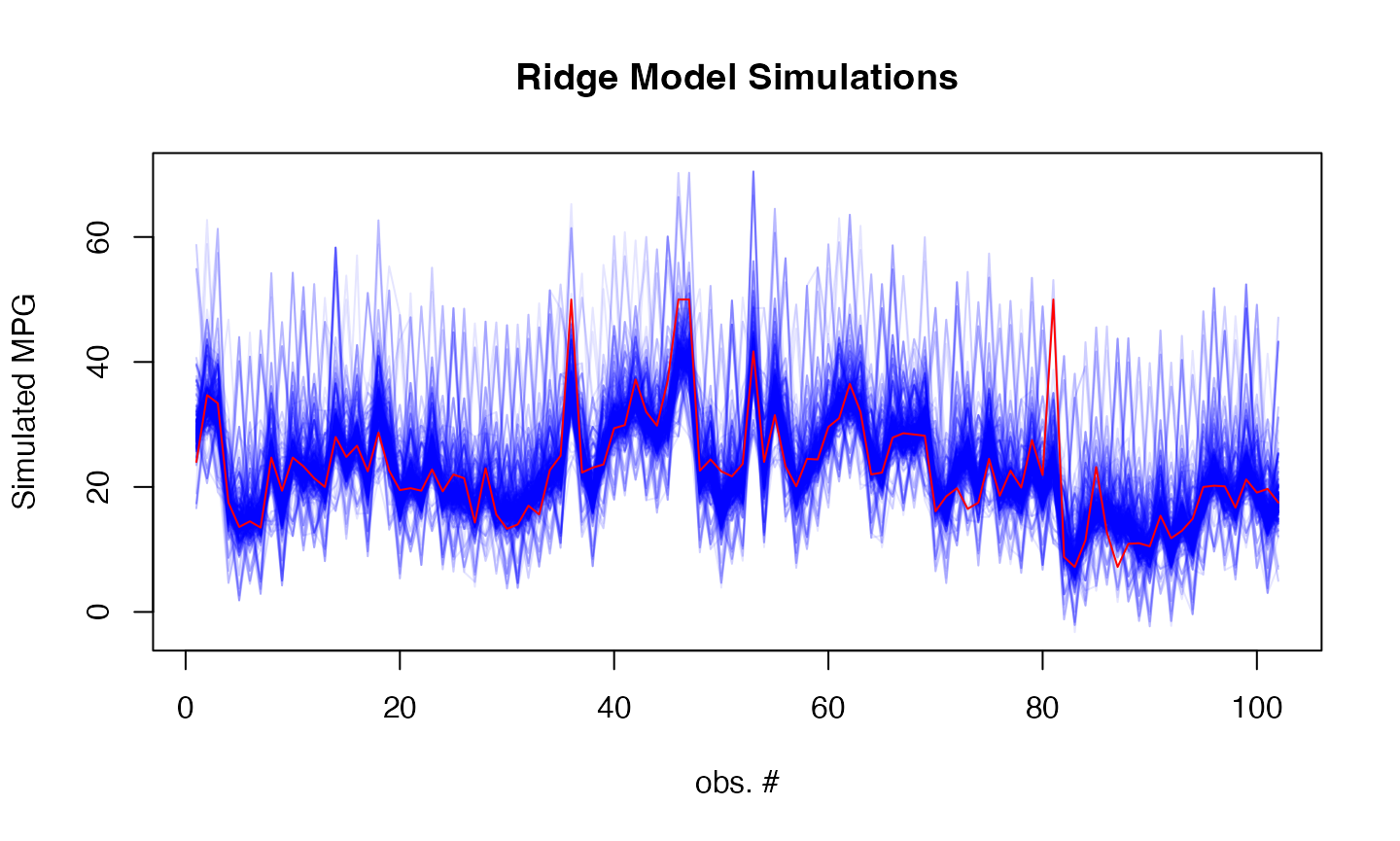
Example 3: Car Price Analysis (Cars93 dataset)
Load and prepare data
data(Cars93, package = "MASS")
# Remove rows with missing values
Cars93 <- na.omit(Cars93)
# Select numeric predictors and price as response
predictors <- c("MPG.city", "MPG.highway", "EngineSize", "Horsepower",
"RPM", "Rev.per.mile", "Fuel.tank.capacity", "Length",
"Wheelbase", "Width", "Turn.circle", "Weight")
car_data <- Cars93[, c(predictors, "Price")]
set.seed(1243)
train_idx <- sample(nrow(car_data), size = floor(0.8 * nrow(car_data)))
train_data <- car_data[train_idx, ]
test_data <- car_data[-train_idx, -which(names(car_data) == "Price")]Fit models
# Fit regular linear model
start <- proc.time()[3]
lm_model <- lm(Price ~ ., data = train_data)
print(proc.time()[3] - start)## elapsed
## 0.028##
## Call:
## lm(formula = Price ~ ., data = train_data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -8.9444 -3.4879 -0.0823 2.5740 10.7036
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 6.0285088 31.8235292 0.189 0.8505
## MPG.city -0.3069383 0.4798163 -0.640 0.5252
## MPG.highway -0.0041568 0.4591254 -0.009 0.9928
## EngineSize 2.4810783 2.4779636 1.001 0.3213
## Horsepower 0.1016741 0.0446071 2.279 0.0268 *
## RPM 0.0001602 0.0023006 0.070 0.9448
## Rev.per.mile 0.0049762 0.0026868 1.852 0.0697 .
## Fuel.tank.capacity -0.1866149 0.5198553 -0.359 0.7211
## Length 0.0203242 0.1333518 0.152 0.8795
## Wheelbase 0.4888949 0.2655782 1.841 0.0713 .
## Width -0.8957689 0.4446575 -2.015 0.0491 *
## Turn.circle -0.3835124 0.3579624 -1.071 0.2889
## Weight 0.0041302 0.0059593 0.693 0.4914
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 4.731 on 52 degrees of freedom
## Multiple R-squared: 0.7886, Adjusted R-squared: 0.7398
## F-statistic: 16.16 on 12 and 52 DF, p-value: 1.548e-13## 2.5 % 97.5 %
## (Intercept) -5.783007e+01 69.887091986
## MPG.city -1.269760e+00 0.655883438
## MPG.highway -9.254594e-01 0.917145804
## EngineSize -2.491319e+00 7.453475962
## Horsepower 1.216348e-02 0.191184768
## RPM -4.456410e-03 0.004776746
## Rev.per.mile -4.152533e-04 0.010367616
## Fuel.tank.capacity -1.229781e+00 0.856550981
## Length -2.472657e-01 0.287914102
## Wheelbase -4.402679e-02 1.021816593
## Width -1.788039e+00 -0.003498354
## Turn.circle -1.101817e+00 0.334791684
## Weight -7.828121e-03 0.016088453
# Fit calibrated model
start <- proc.time()[3]
svm_model <- rvfl::calibmodel(lambda=10**seq(-10, 10, length.out=100), x = as.matrix(train_data[,-which(names(train_data) == "Price")]),
y = train_data$Price, engine = glmGamma)
print(proc.time()[3] - start)## elapsed
## 0.097##
## Call:
## svm(formula = formula, data = ..1)
##
##
## Parameters:
## SVM-Type: eps-regression
## SVM-Kernel: radial
## cost: 1
## gamma: 0.08333333
## epsilon: 0.1
##
##
## Number of Support Vectors: 37Make predictions and compare
results <- data.frame(
Actual = car_data[-train_idx, "Price"],
LM_Pred = lm_pred[,"fit"],
LM_Lower = lm_pred[,"lwr"],
LM_Upper = lm_pred[,"upr"],
svm_Pred = svm_pred[,"fit"],
svm_Lower = svm_pred[,"lwr"],
svm_Upper = svm_pred[,"upr"]
)
# Print results
print("Prediction Intervals Comparison:")## [1] "Prediction Intervals Comparison:"
print(results)## Actual LM_Pred LM_Lower LM_Upper svm_Pred svm_Lower svm_Upper
## 7 20.8 22.284761 12.3951390 32.17438 24.644307 17.807962 43.33853
## 12 13.4 14.354853 3.3289673 25.38074 11.674070 4.883566 30.36830
## 15 15.9 17.852333 7.2347759 28.46989 16.590922 10.534942 36.07882
## 21 15.8 19.516709 9.4219263 29.61149 18.463087 11.904269 34.04776
## 23 9.2 14.340649 3.5068316 25.17447 13.462951 6.904134 31.68293
## 29 12.2 9.028432 -1.4360619 19.49293 10.021731 3.476222 28.24171
## 30 19.3 29.775630 19.1961282 40.35513 23.626379 16.776725 42.32061
## 31 7.4 6.013838 -5.5354656 17.56314 12.873051 6.023397 30.80219
## 32 10.1 14.806645 4.1551453 25.45814 14.838166 8.133931 32.91272
## 42 12.1 8.704607 -3.6984146 21.10763 13.314959 6.756141 31.53493
## 54 11.6 10.002970 -0.3839704 20.38991 9.754851 3.209342 28.73991
## 59 61.9 34.711053 24.1509123 45.27119 22.914288 16.414621 38.49896
## 72 14.4 9.110664 -1.1222765 19.34360 12.453800 5.578156 31.12204
## 73 9.0 11.005860 0.0448295 21.96689 10.922573 4.060237 29.59081
## 76 18.5 26.775186 16.6537717 36.89660 23.760965 16.911311 39.05481
## 91 23.3 24.122428 12.0542302 36.19063 20.927726 14.078073 39.62195
## 92 22.7 18.531114 8.4532906 28.60894 16.130723 9.571905 34.35070
# Calculate coverage and Winkler scores
lm_coverage <- mean(car_data[-train_idx, "Price"] >= results$LM_Lower &
car_data[-train_idx, "Price"] <= results$LM_Upper)
svm_coverage <- mean(car_data[-train_idx, "Price"] >= results$svm_Lower &
car_data[-train_idx, "Price"] <= results$svm_Upper)
lm_winkler <- misc::winkler_score(car_data[-train_idx, "Price"], results$LM_Lower, results$LM_Upper)
svm_winkler <- misc::winkler_score(car_data[-train_idx, "Price"], results$svm_Lower, results$svm_Upper)
print(sprintf("\nPrediction interval metrics:"))## [1] "\nPrediction interval metrics:"
print(sprintf("Linear Model: %.1f%% coverage, %.3f Winkler score",
100 * lm_coverage, mean(lm_winkler)))## [1] "Linear Model: 94.1% coverage, 60.599 Winkler score"
print(sprintf("Calibrated Model: %.1f%% coverage, %.3f Winkler score",
100 * svm_coverage, mean(svm_winkler)))## [1] "Calibrated Model: 94.1% coverage, 79.725 Winkler score"
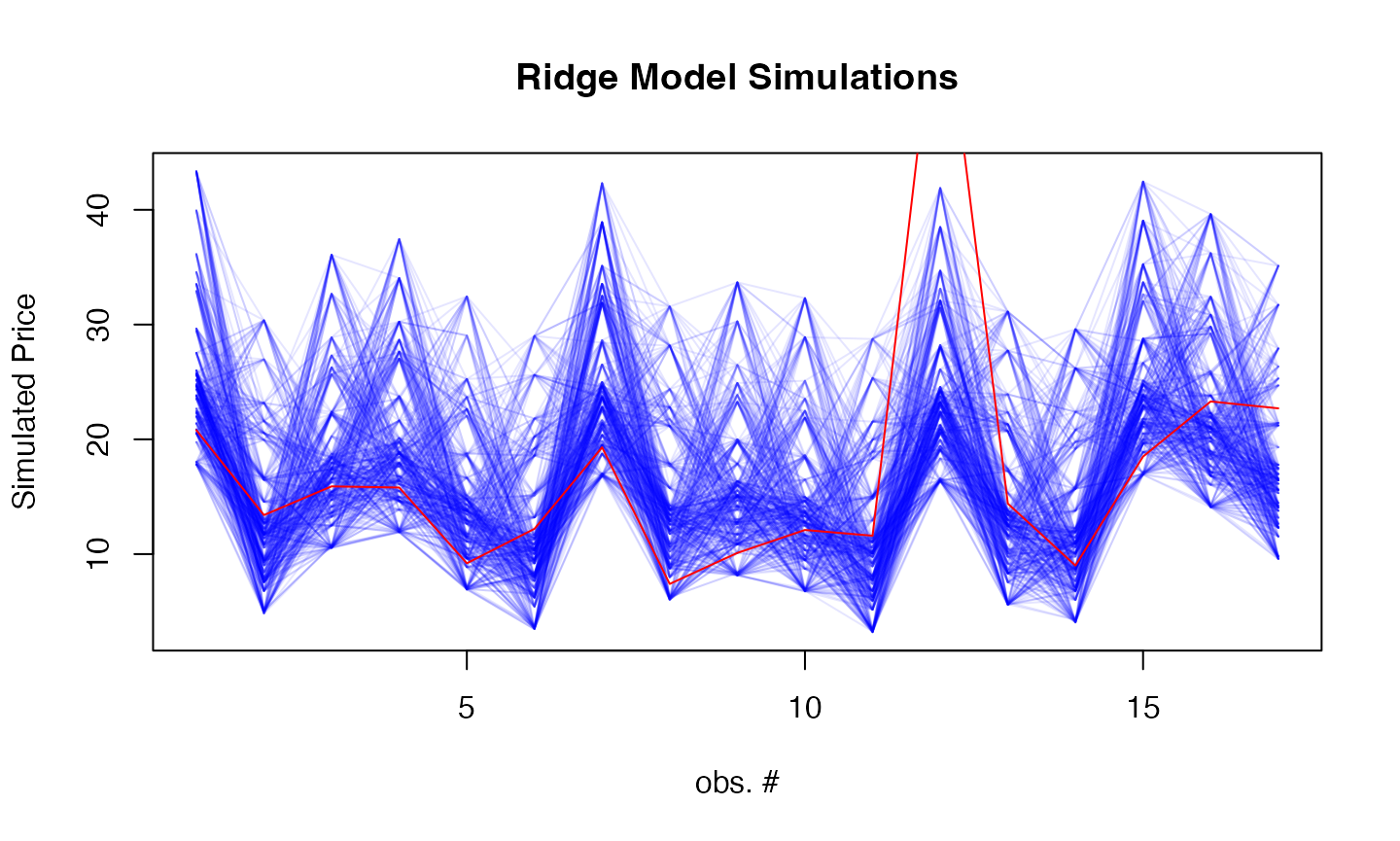
sims <- simulate(svm_model, newdata = as.matrix(test_data), nsim = 500, method="bootstrap")
# Plot simulations
matplot(sims, type = "l",
col = rgb(0, 0, 1, 0.1), lty = 1,
xlab = "obs. #", ylab = "Simulated Price",
main = "Ridge Model Simulations")
lines(car_data[-train_idx, "Price"], col = "red")