Beyond GARCH

Introduction

Probabilistic stock forecasting often relies on parametric models like ARIMA for the mean and GARCH for volatility. The mlarchf function in the ahead package offers a flexible hybrid alternative to ARMA-GARCH by combining machine learning approaches with ARCH effects.

The model decomposes the time series into two components:

1. Mean component: $y_t = \mu_t + \sigma_t \varepsilon_t$
2. Volatility component: $\sigma_t^2 = f(\varepsilon_{t-1}^2, \varepsilon_{t-2}^2, ...)$

where:

• $\mu_t$ is the conditional mean (modeled using any forecasting method)
• $\sigma_t$ is the conditional volatility (modeled using machine learning)
• $\varepsilon_t$ are standardized residuals

The key innovation is using machine learning methods and conformal prediction to model the volatility component, allowing for more flexible and potentially more accurate volatility forecasts than traditional GARCH models. The function supports various machine learning methods through parameters fit_func and predict_func as in other ahead models, and through the caret package.

The forecasting process involves:

• Fitting a mean model (default: auto.arima)
• Modeling the squared residuals using machine learning. For this to work, the residuals from the mean model need to be centered, so that

$$\mathbb{E}[\epsilon_t^2|F_{t-1}]$$

(basically a supervised regression of squared residuals on their lags) is a good approximation of the latent conditional volatility

• Conformalizing the standardized residuals for prediction intervals

This new approach combines the interpretability of traditional time series models with the flexibility of machine learning, while maintaining proper uncertainty quantification through conformal prediction.

Basic Usage

Let’s start with a simple example using the Google stock price data from the fpp2 package:

y <- fpp2::goog200

# Default model for volatility (Ridge regression for volatility)
(obj_ridge <- ahead::mlarchf(y, h=20L, B=500L))

##     Point Forecast    Lo 95    Hi 95
## 201       534.4214 513.0126 549.3933
## 202       536.2434 516.2732 554.8150
## 203       536.4303 521.4628 553.5272
## 204       536.6375 516.4954 559.5297
## 205       536.9744 513.3218 555.6087
## 206       536.8669 518.1739 552.4974
## 207       539.0674 519.1329 558.1132
## 208       537.4618 501.6436 560.6395
## 209       540.1076 518.9179 558.1104
## 210       536.5789 509.1344 555.3092
## 211       540.7064 517.4373 555.1692
## 212       543.6837 528.5274 561.0367
## 213       543.4614 524.3126 564.4024
## 214       544.3046 526.8852 564.2636
## 215       544.1797 522.0492 560.9355
## 216       544.7224 525.9826 560.9314
## 217       545.7186 524.2705 564.2966
## 218       546.5558 524.4960 568.5002
## 219       546.0634 527.0138 562.9881
## 220       548.5014 525.1081 567.3897

Different Machine Learning Methods

The package supports various machine learning methods for volatility modeling. Here are some examples:

# Random Forest
(obj_rf <- ahead::mlarchf(y, fit_func = randomForest::randomForest, 
                     predict_func = predict, h=20L, B=500L))

##     Point Forecast    Lo 95    Hi 95
## 201       534.1512 510.3324 552.3963
## 202       536.2532 513.0656 559.3006
## 203       535.9461 519.9620 552.2986
## 204       537.0154 510.5593 566.3488
## 205       536.6587 511.9640 557.5270
## 206       536.8918 511.8123 557.0593
## 207       538.5116 516.4982 559.0598
## 208       537.6690 500.2783 558.3135
## 209       539.8688 513.5599 560.6459
## 210       537.2253 509.0348 559.8301
## 211       540.5074 518.2870 556.2040
## 212       543.2205 524.8324 565.9389
## 213       542.9070 520.6425 563.8805
## 214       544.3180 522.2758 568.1577
## 215       543.7810 521.8650 560.4342
## 216       544.6455 525.4243 562.8774
## 217       545.5607 520.4664 565.2332
## 218       546.2067 522.8465 571.9418
## 219       545.8613 526.1130 562.6742
## 220       548.4096 527.0026 569.4774

# Support Vector Machine
(obj_svm <- ahead::mlarchf(y, fit_func = e1071::svm, 
                     predict_func = predict, h=20L, B=500L))

##     Point Forecast    Lo 95    Hi 95
## 201       533.7170 517.3170 544.6631
## 202       534.6215 524.3793 544.5595
## 203       536.5179 520.7747 553.2203
## 204       536.5351 517.2433 558.2349
## 205       536.8402 515.4246 554.3359
## 206       536.7315 520.3277 550.1107
## 207       538.3551 522.7912 553.1115
## 208       537.7272 487.5047 570.7947
## 209       539.5938 523.3432 554.6829
## 210       537.3854 520.4736 549.0138
## 211       540.6617 518.7450 556.5441
## 212       543.1811 530.3252 560.4024
## 213       542.8325 525.8313 560.2181
## 214       543.1528 531.3217 555.5522
## 215       543.6781 526.0638 556.7800
## 216       544.9585 524.4062 564.1614
## 217       545.0948 529.2871 558.7188
## 218       545.6335 530.3653 560.2707
## 219       546.0660 526.8957 563.5162
## 220       548.2219 527.1229 565.0835

# Elastic Net
(obj_glmnet <- ahead::mlarchf(y, fit_func = glmnet::cv.glmnet, 
                     predict_func = predict, h=20L, B=500L))

##     Point Forecast    Lo 95    Hi 95
## 201       534.7928 510.4350 551.7094
## 202       536.3282 515.8595 555.3620
## 203       536.6786 520.3420 555.3749
## 204       536.2580 517.9287 555.7452
## 205       537.1529 511.5610 557.0738
## 206       536.9223 517.4544 553.2179
## 207       539.0651 520.2480 558.3500
## 208       537.4080 504.0407 558.9956
## 209       540.0442 519.4301 557.5566
## 210       536.4339 506.9348 556.5256
## 211       540.6602 517.7029 554.8026
## 212       543.6814 528.5776 560.8094
## 213       543.4691 524.3082 564.4681
## 214       544.3872 527.1408 564.8278
## 215       544.1525 521.6824 560.8221
## 216       544.7067 525.9955 561.3552
## 217       545.7233 524.1913 564.3838
## 218       546.5761 523.1143 568.8639
## 219       546.0707 526.9582 563.1625
## 220       548.4857 525.2693 567.3683

Let’s visualize the forecasts:

par(mfrow=c(1, 2))
plot(obj_ridge, main="Ridge Regression")
plot(obj_rf, main="Random Forest")

par(mfrow=c(1, 2))
plot(obj_svm, main="Support Vector Machine")
plot(obj_glmnet, main="Elastic Net")

Using caret Models

The package also supports models from the caret package, which provides access to hundreds of machine learning methods. Here’s how to use them:

y <- window(fpp2::goog200, start=100)

# Random Forest via caret
(obj_rf <- ahead::mlarchf(y, ml_method="ranger", h=20L))

##     Point Forecast    Lo 95    Hi 95
## 201       531.9962 519.6288 542.0442
## 202       533.5966 501.3078 567.1908
## 203       532.3779 515.7682 541.3345
## 204       533.2071 499.3026 555.6130
## 205       532.4515 522.4715 541.8420
## 206       530.9037 499.3297 554.6568
## 207       532.8339 523.5267 540.7952
## 208       535.0550 492.9833 575.9206
## 209       532.7999 514.8486 548.6330
## 210       532.0662 509.0840 547.3646
## 211       532.9558 520.1173 545.3782
## 212       534.4784 518.5097 561.1701
## 213       533.4831 514.4327 550.3137
## 214       531.6962 507.7971 544.7853
## 215       532.0200 514.4460 546.2595
## 216       532.7877 519.3994 543.1369
## 217       533.7333 519.4345 545.4001
## 218       532.5218 518.5863 545.3066
## 219       532.5714 515.5647 548.8354
## 220       532.3071 512.3712 547.3188

# Gradient Boosting via caret
(obj_glmboost <- ahead::mlarchf(y, ml_method="glmboost", h=20L))

##     Point Forecast    Lo 95    Hi 95
## 201       532.1232 515.6045 546.6549
## 202       533.0962 506.5413 559.6886
## 203       533.8033 490.7712 558.3938
## 204       532.8558 502.4099 553.7752
## 205       534.3695 505.3856 563.0579
## 206       530.9396 506.2500 550.3506
## 207       534.9237 510.1448 555.6755
## 208       534.8340 494.8246 572.1718
## 209       533.2415 507.1893 555.7273
## 210       532.0511 504.8738 550.3687
## 211       533.6957 516.0999 552.7027
## 212       534.8749 515.1305 564.9202
## 213       534.0364 507.5508 556.0636
## 214       531.7777 495.7765 551.1185
## 215       532.2214 508.2610 552.0268
## 216       533.4324 514.2235 549.0329
## 217       534.8546 512.1173 551.4156
## 218       533.2181 509.9089 554.2609
## 219       533.0263 508.3742 557.0509
## 220       532.7730 505.0416 557.1151

# Gradient Boosting via caret and using clustering explicitly
(obj_glmboost2 <- ahead::mlarchf(y, ml_method="glmboost", n_clusters=2, h=20L))

##     Point Forecast    Lo 95    Hi 95
## 201       532.1621 514.6453 547.5720
## 202       533.0470 507.2998 558.8306
## 203       533.7865 491.0647 558.1997
## 204       533.1064 497.1227 557.8308
## 205       534.2077 506.8464 561.2900
## 206       530.8846 503.6745 552.2772
## 207       534.5441 512.4951 553.0098
## 208       535.2795 489.9581 577.5747
## 209       533.0794 509.4218 553.4985
## 210       532.1277 501.3159 552.8949
## 211       533.4410 517.8666 550.2643
## 212       534.5712 516.5925 561.9293
## 213       533.8342 509.4415 554.1208
## 214       531.7457 499.5986 549.0159
## 215       532.1561 510.3004 550.2219
## 216       533.2083 516.2028 547.0191
## 217       534.6233 513.4436 550.0499
## 218       533.0719 511.7212 552.3466
## 219       532.8965 510.3113 554.9069
## 220       532.6787 506.9663 555.2486

(obj_glmboost3 <- ahead::mlarchf(y, ml_method="glmboost", n_clusters=3, h=20L))

##     Point Forecast    Lo 95    Hi 95
## 201       532.1033 516.0923 546.1886
## 202       533.0416 507.3835 558.7359
## 203       533.7744 491.2756 558.0603
## 204       533.0548 498.2120 556.9952
## 205       534.2518 506.4483 561.7718
## 206       530.9297 505.7850 550.6984
## 207       534.5671 512.3527 553.1713
## 208       534.9336 493.7363 573.3800
## 209       533.0175 510.2750 552.6467
## 210       532.0657 504.1946 550.8510
## 211       533.3837 518.2637 549.7163
## 212       534.5108 516.8830 561.3350
## 213       533.7617 510.1196 553.4242
## 214       531.7399 500.2805 548.6408
## 215       532.1503 510.4822 550.0609
## 216       533.1919 516.3476 546.8718
## 217       534.5654 513.7757 549.7078
## 218       533.0520 511.9678 552.0861
## 219       532.8724 510.6714 554.5082
## 220       532.6660 507.2260 554.9967

Visualizing the forecasts:

par(mfrow=c(1, 2))
plot(obj_rf, main="Random Forest (caret)")
plot(obj_glmboost, main="Gradient Boosting (caret)")

par(mfrow=c(1, 2))
plot(obj_glmboost2, main="Gradient Boosting (caret) \n 2 clusters")
plot(obj_glmboost3, main="Gradient Boosting (caret) \n 3 clusters")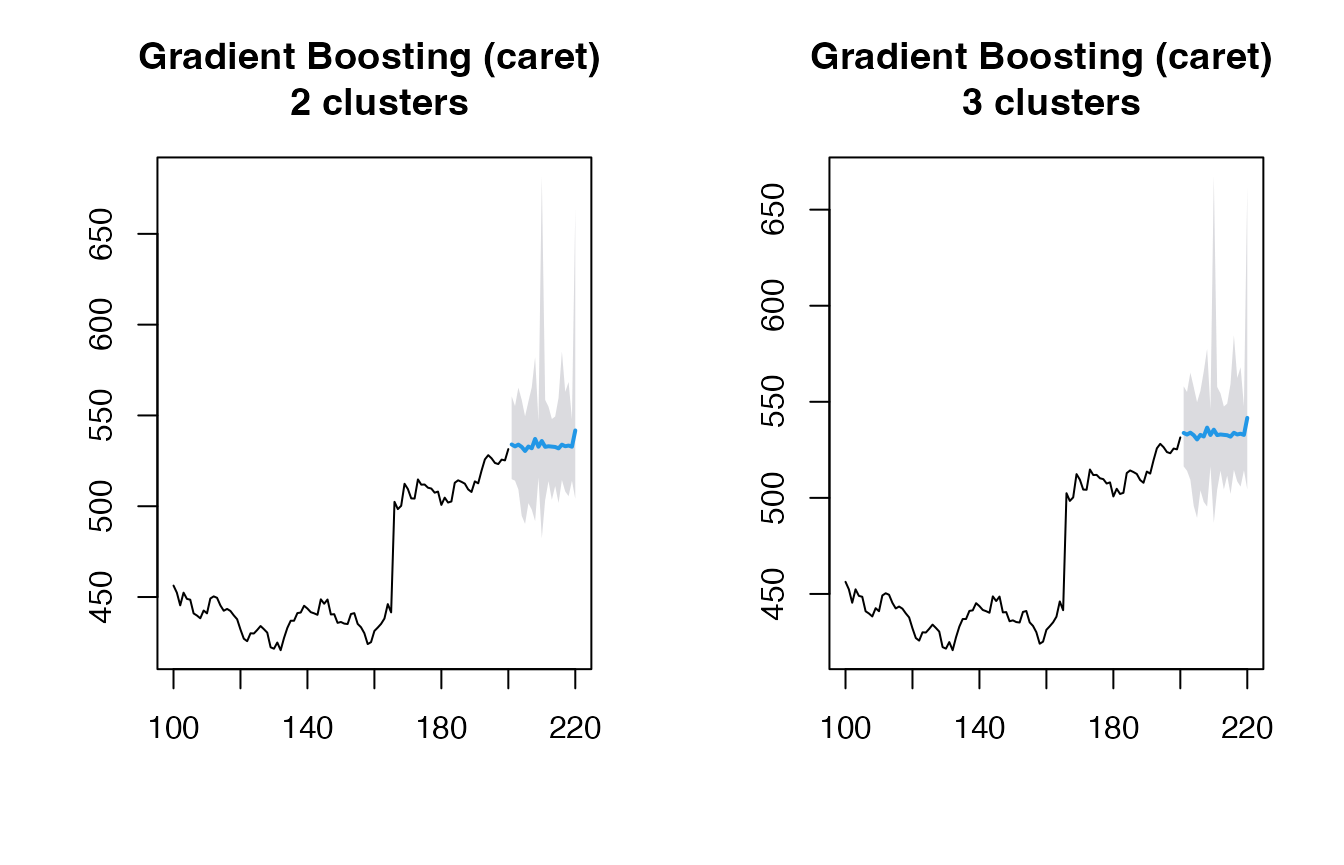

Looking at the simulation paths:

par(mfrow=c(1, 2))
matplot(obj_rf$sims, type='l', main="RF Simulation Paths")
matplot(obj_glmboost$sims, type='l', main="GBM Simulation Paths")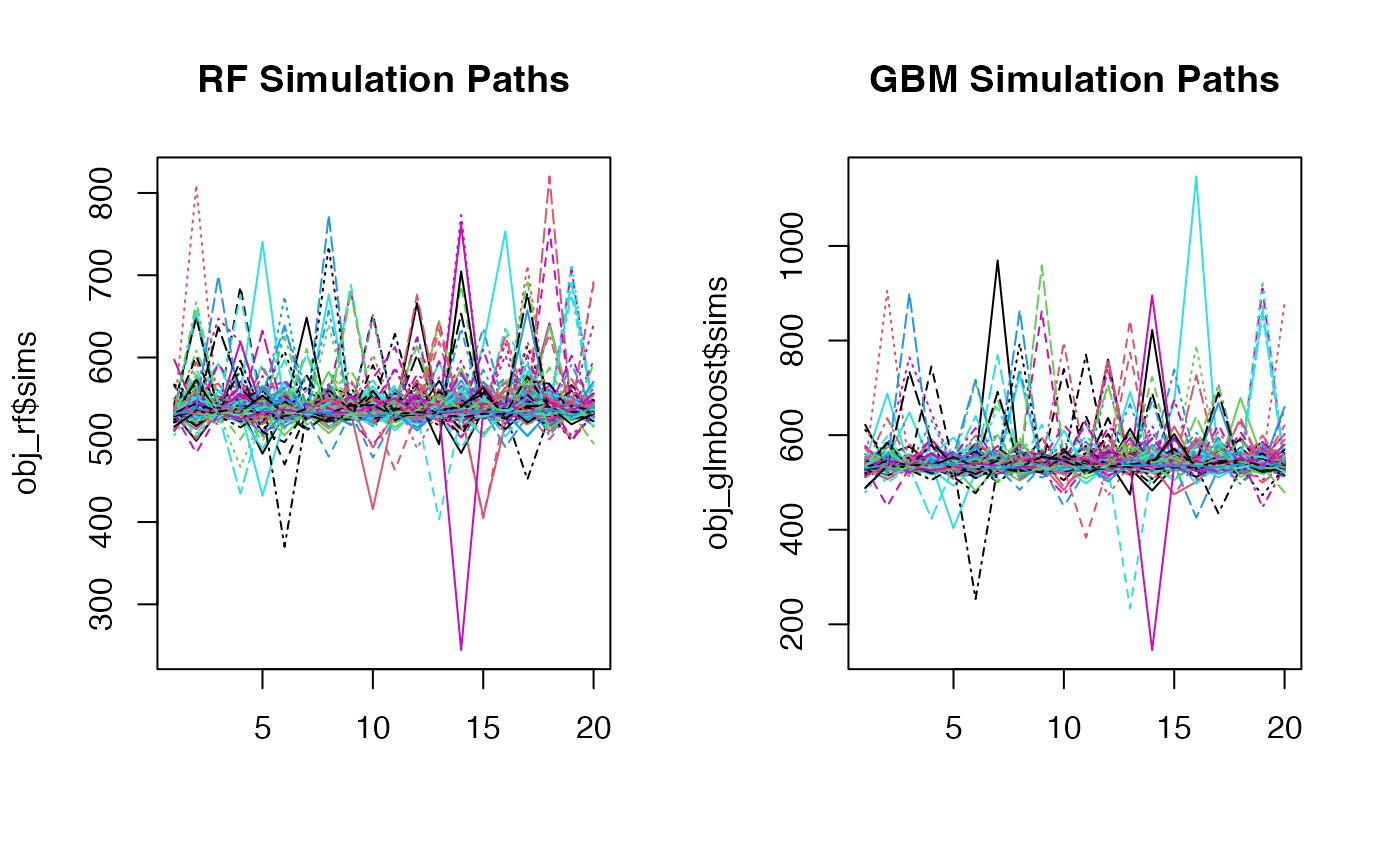

Customizing Mean and Residual Models

You can also customize both the mean forecasting model and the model for forecasting standardized residuals:

# Using RW + Theta method for mean and residuals along with SVM for volatility
(obj_svm <- ahead::mlarchf(y, fit_func = e1071::svm, 
                     predict_func = predict, h=20L, 
                     mean_model=forecast::rwf,
                     model_residuals=forecast::thetaf))

##     Point Forecast    Lo 95    Hi 95
## 201       534.5275 525.6794 550.5503
## 202       539.9297 511.3076 586.5338
## 203       535.6107 520.6631 553.3606
## 204       539.8380 511.2234 574.8781
## 205       535.3418 526.2796 551.4300
## 206       536.4786 518.2886 560.0783
## 207       534.7621 527.1816 544.1724
## 208       541.9045 513.7523 607.6621
## 209       535.7972 525.7187 552.7226
## 210       538.3410 514.6493 565.7574
## 211       536.4844 526.9339 556.1342
## 212       544.0718 521.0150 594.9118
## 213       537.7204 522.5539 564.8411
## 214       540.7948 516.5959 584.6435
## 215       535.7706 523.0148 557.4264
## 216       540.2827 522.6870 577.0492
## 217       538.8013 526.4015 565.2776
## 218       539.9638 523.7616 572.1950
## 219       538.6039 527.1762 570.1166
## 220       541.1636 518.1337 592.9968

# Using Theta + Theta method for mean and residuals along with GLMNET for volatility
(obj_glmnet <- ahead::mlarchf(y, fit_func = glmnet::cv.glmnet, 
                     predict_func = predict, h=20L, 
                     mean_model=forecast::thetaf,
                     model_residuals=forecast::thetaf))

##     Point Forecast    Lo 95    Hi 95
## 201       536.9599 520.8207 560.6615
## 202       537.7893 520.1798 566.0057
## 203       539.5527 515.5745 574.9838
## 204       538.1037 523.1747 555.6820
## 205       540.3120 524.2845 565.2594
## 206       539.2865 523.2293 566.6387
## 207       541.9672 526.7464 562.5389
## 208       543.3955 522.6309 605.3702
## 209       542.8862 523.6645 569.4162
## 210       541.8687 526.0819 562.2838
## 211       544.3955 530.7274 580.4541
## 212       545.3069 532.5605 578.1298
## 213       545.5162 528.4423 578.4759
## 214       545.9000 527.6103 588.7563
## 215       544.7800 527.1494 571.4776
## 216       545.6953 531.3418 565.1566
## 217       548.4279 534.1135 575.3197
## 218       547.0435 533.7407 573.0924
## 219       549.6855 533.0437 595.3706
## 220       548.4694 533.1184 581.8005

plot(obj_svm, main="SVM with RW + Theta")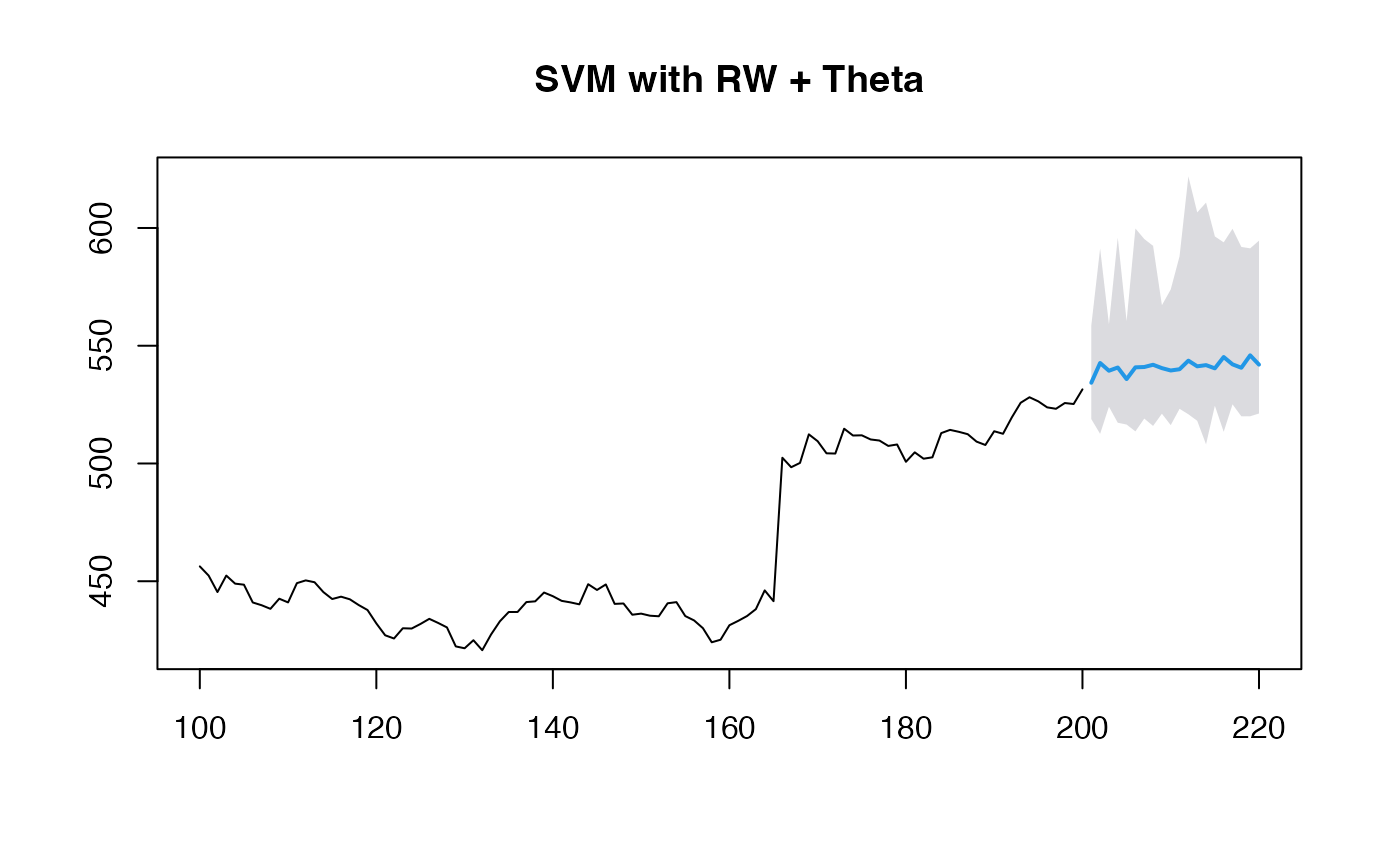

plot(obj_glmnet, main="Elastic Net with Theta + Theta")

When using non-ARIMA models for the mean forecast, it’s important to check if the residuals of the mean forecasting model are centered and stationary:

# Diagnostic tests for residuals
print(obj_svm$resids_t_test)

## 
##  One Sample t-test
## 
## data:  resids
## t = 1.0148, df = 99, p-value = 0.3127
## alternative hypothesis: true mean is not equal to 0
## 95 percent confidence interval:
##  -0.7180739  2.2214961
## sample estimates:
## mean of x 
## 0.7517111

print(obj_svm$resids_kpss_test)

## 
##  KPSS Test for Level Stationarity
## 
## data:  resids
## KPSS Level = 0.25344, Truncation lag parameter = 4, p-value = 0.1

print(obj_glmnet$resids_t_test)

## 
##  One Sample t-test
## 
## data:  resids
## t = 1.0992, df = 100, p-value = 0.2743
## alternative hypothesis: true mean is not equal to 0
## 95 percent confidence interval:
##  -0.6460748  2.2513707
## sample estimates:
## mean of x 
## 0.8026479

print(obj_glmnet$resids_kpss_test)

## 
##  KPSS Test for Level Stationarity
## 
## data:  resids
## KPSS Level = 0.26089, Truncation lag parameter = 4, p-value = 0.1