## Loading required package: ggplot2
## Loading required package: gridExtra
## Loading required package: reshape2
## Loading required package: VineCopula
## Loading required package: randtoolbox
## Loading required package: rngWELL
## This is randtoolbox. For an overview, type 'help("randtoolbox")'.
##
##
## This is version 1.3.0 of esgtoolkit. Starting with 1.0.0, package renamed as: 'esgtoolkit' (lowercase)
##
##
# Spot variance
V0 <- 0.1372
# mean-reversion speed
kappa <- 9.5110/100
# long-term variance
theta <- 0.0285
# volatility of volatility
volvol <- 0.8010/100
# Correlation between stoch. vol and prices
rho <- -0.5483
# Intensity of the Poisson process
lambda <- 0.3635
# mean and vol of the merton jumps diffusion
mu_J <- -0.2459
sigma_J <- 0.2547/100
m <- exp(mu_J + 0.5*(sigma_J^2)) - 1
# Initial stock price
S0 <- 4468.17
# Initial short rate
r0 <- 0.0357
# ============================================================================
# SIMULATION SETUP
# ============================================================================
n <- 300
horizon <- 1
freq <- "weekly"
start_ <- start(EuStockMarkets)
end_ <- end(EuStockMarkets)
print(end_ - start_)
## [1] 7 39
freq_ <- frequency(EuStockMarkets)
# Simulation of shocks, with antithetic variates
shocks <- esgtoolkit::simshocks(n = n,
horizon = 8L,
method = "anti",
family = 1, par = rho,
start = start_, frequency=freq_)
print(start_)
## [1] 1991 130
## [1] 260
## [1] 1998 169
## [1] 1991 130
## [1] 260
## [1] 1999 129
============================================================================
VOLATILITY SIMULATION (CIR PROCESS)
============================================================================
# Vol simulation
sim_vol <- esgtoolkit::simdiff(n = n,
model = "CIR", x0 = V0,
theta1 = kappa*theta, theta2 = kappa,
theta3 = volvol,
eps = shocks[[1]],
start = start_,
frequency=freq_,
horizon = 8L)
print(start(sim_vol))
## [1] 1991 130
## [1] 260
## [1] 1999 130
============================================================================
ASSET PRICE SIMULATION (GBM WITH JUMPS)
============================================================================
# prices simulation
sim_price <- esgtoolkit::simdiff(n = n, start = start_,
end = end_,
frequency=freq_,
horizon = 8L,
model = "GBM", x0 = S0,
theta1 = r0 - lambda*m, theta2 = sim_vol,
lambda = lambda, mu_z = mu_J,
sigma_z = sigma_J,
eps = shocks[[2]])
print(start(sim_price))
## [1] 1991 130
## [1] 260
## [1] 1998 169
## [1] 1860 300
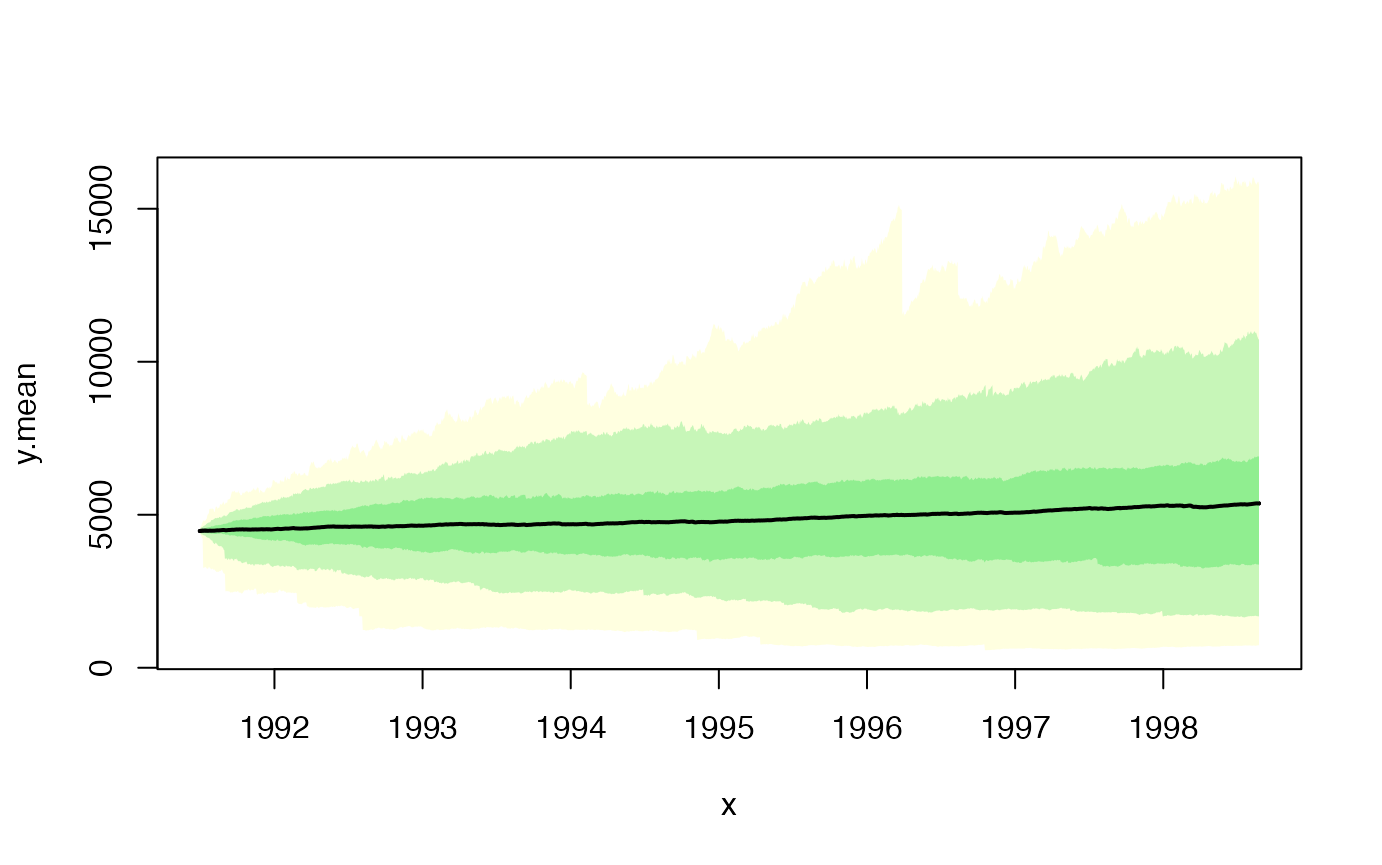
# Plot the simulated price paths
esgtoolkit::esgplotbands(sim_price)